Zavedení
V předchozí kapitole bylo ukázáno, že lze snadno získat přesné matematické situace pro síly vyvíjené kapalinami v klidu. Je to proto, že v hydrostatice se jedná pouze o jednoduché tlakové síly. Pokud se uvažuje kapalina v pohybu, problém analýzy se okamžitě stává mnohem obtížnějším. Je třeba vzít v úvahu nejen velikost a směr rychlosti částic, ale také komplexní vliv viskozity, která způsobuje smykové nebo třecí napětí mezi pohybujícími se částicemi kapaliny a na jejich hranicích. Relativní pohyb, který je možný mezi různými prvky tekutého tělesa, způsobuje, že se tlak a smykové napětí značně mění od jednoho bodu k druhému v závislosti na podmínkách proudění. Vzhledem ke složitosti spojené s jevem proudění je přesná matematická analýza možná pouze v několika málo, a z inženýrského hlediska i v některých nepraktických případech. Proto je nutné řešit problémy proudění buď experimentálně, nebo stanovením určitých zjednodušujících předpokladů dostatečných k získání teoretického řešení. Tyto dva přístupy se vzájemně nevylučují, protože základní zákony mechaniky platí vždy a umožňují použití částečně teoretických metod v několika důležitých případech. Je také důležité experimentálně zjistit rozsah odchylky od skutečných podmínek v důsledku zjednodušené analýzy.
Nejběžnějším zjednodušujícím předpokladem je, že tekutina je ideální nebo dokonalá, čímž se eliminují komplikující viskózní efekty. Toto je základ klasické hydrodynamiky, odvětví aplikované matematiky, které věnovali pozornost významní vědci, jako jsou Stokes, Rayleigh, Rankine, Kelvin a Lamb. Klasická teorie má vážná inherentní omezení, ale protože voda má relativně nízkou viskozitu, chová se v mnoha situacích jako skutečná tekutina. Z tohoto důvodu lze klasickou hydrodynamiku považovat za velmi cenný základ pro studium charakteristik pohybu tekutin. Tato kapitola se zabývá základní dynamikou pohybu tekutin a slouží jako základní úvod k následujícím kapitolám zabývajícím se specifičtějšími problémy, s nimiž se setkáváme ve stavební hydraulice. Jsou odvozeny tři důležité základní rovnice pohybu tekutin, a to rovnice kontinuity, Bernoulliho rovnice a rovnice hybnosti, a je vysvětlen jejich význam. Později jsou zvažována omezení klasické teorie a popsáno chování skutečné tekutiny. V celém textu se předpokládá nestlačitelná tekutina.
Typy proudění
Různé typy pohybu tekutin lze rozdělit následovně:
1. Turbulentní a laminární
2. Rotační a nerotační
3. Stabilní a nestabilní
4. Jednotné a nejednotné.
Ponorné čerpadlo na odpadní vodu
Axiální čerpadla řady MVS Smíšená čerpadla řady AVS (vertikální axiální a smíšená ponorná čerpadla na odpadní vodu) jsou moderní výrobky, které byly úspěšně navrženy s využitím moderních zahraničních technologií. Kapacita nových čerpadel je o 20 % větší než u starých. Účinnost je o 3–5 % vyšší než u starých čerpadel.

Turbulentní a laminární proudění.
Tyto termíny popisují fyzikální podstatu proudění.
V turbulentním proudění je postup částic tekutiny nepravidelný a dochází k zdánlivě nahodilé výměně poloh. Jednotlivé částice jsou vystaveny kolísavým příčným rychlostem, takže pohyb je spíše vířivý a klikatý než přímočarý. Pokud je barvivo vstřikováno v určitém bodě, rychle se rozptýlí v celém proudu. Například v případě turbulentního proudění v potrubí by okamžitý záznam rychlosti v daném úseku odhalil přibližné rozložení, jak je znázorněno na obrázku 1(a). Ustálená rychlost, jak by byla zaznamenána běžnými měřicími přístroji, je znázorněna tečkovaným obrysem a je zřejmé, že turbulentní proudění je charakterizováno nestacionární kolísavou rychlostí superponovanou na časově ustálený průměr.
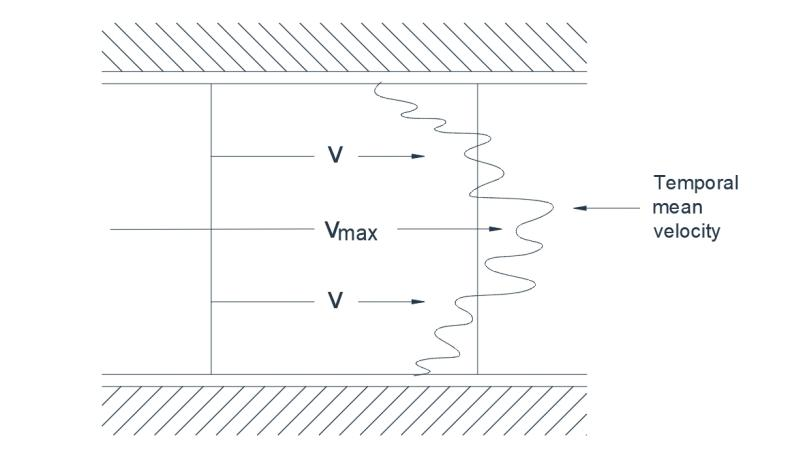
Obr. 1(a) Turbulentní proudění
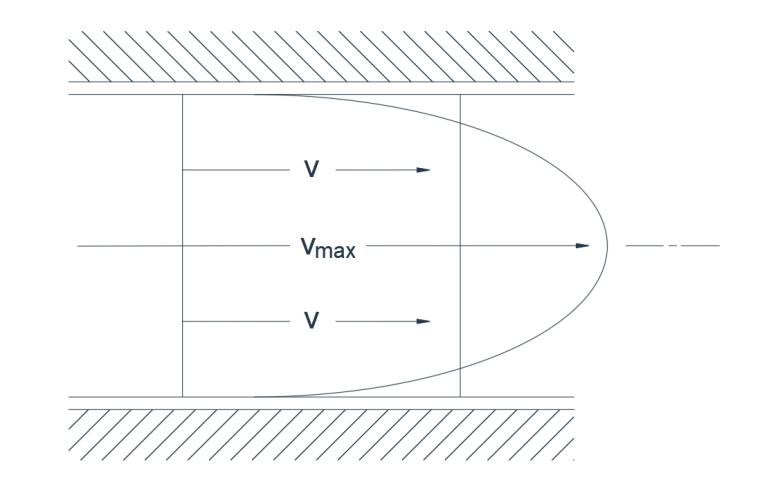
Obr. 1(b) Laminární proudění
V laminárním proudění se všechny částice tekutiny pohybují po rovnoběžných drahách a neexistuje žádná příčná složka rychlosti. Uspořádaný postup je takový, že každá částice sleduje přesně dráhu částice, která jí předchází, bez jakékoli odchylky. Tenké vlákno barviva tak zůstane jako takové bez difúze. V laminárním proudění (obr. 1b) je mnohem větší příčný gradient rychlosti než v turbulentním proudění. Například u potrubí je poměr střední rychlosti V a maximální rychlosti Vmax 0,5 při turbulentním proudění a 0,05 při laminárním proudění.
Laminární proudění je spojeno s nízkými rychlostmi a viskózními, pomalu tekoucími kapalinami. V potrubních a otevřených kanálech jsou rychlosti téměř vždy dostatečně vysoké, aby zajistily turbulentní proudění, ačkoli v blízkosti pevné hranice přetrvává tenká laminární vrstva. Zákony laminárního proudění jsou plně pochopeny a pro jednoduché okrajové podmínky lze rozložení rychlosti matematicky analyzovat. Vzhledem ke své nepravidelné pulzující povaze se turbulentní proudění vymyká přísnému matematickému zpracování a pro řešení praktických problémů je nutné se do značné míry spoléhat na empirické nebo semiempirické vztahy.

Vertikální turbínové požární čerpadlo
Číslo modelu: XBC-VTP
Vertikální protipožární čerpadla s dlouhou hřídelí řady XBC-VTP jsou jednostupňová a vícestupňová difuzní čerpadla vyrobená v souladu s nejnovější národní normou GB6245-2006. Vylepšili jsme také konstrukci s odkazem na normu Asociace protipožární ochrany Spojených států. Používají se hlavně pro zásobování vodou v petrochemickém průmyslu, zemním plynu, elektrárnách, bavlněném textilním průmyslu, přístavech, letectví, skladování, výškových budovách a dalších odvětvích. Lze je použít i pro lodě, námořní tanky, požární plavidla a další zásobovací účely.
Rotační a nerotační proudění.
Proudění se nazývá rotační, pokud má každá částice tekutiny úhlovou rychlost kolem svého těžiště.
Obrázek 2a ukazuje typické rozložení rychlosti spojené s turbulentním prouděním za přímou hranicí. V důsledku nerovnoměrného rozložení rychlosti trpí částice, jejíž dvě osy jsou původně kolmé, deformací s malým stupněm rotace. Na obrázku 2a je znázorněno proudění v kruhovém
Je znázorněna dráha, kde rychlost je přímo úměrná poloměru. Dvě osy částice se otáčejí ve stejném směru, takže proudění je opět rotační.
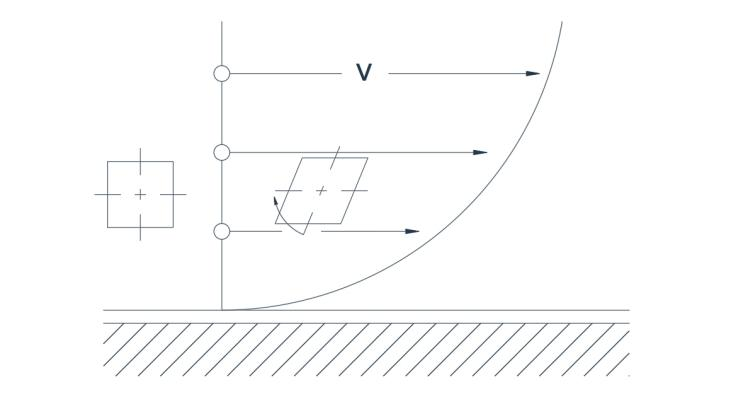
Obr. 2(a) Rotační tok
Aby bylo proudění nerotační, musí být rozložení rychlosti v blízkosti přímé hranice rovnoměrné (obr. 2b). V případě proudění po kruhové dráze lze ukázat, že nerotační proudění bude existovat pouze za předpokladu, že rychlost je nepřímo úměrná poloměru. Na první pohled na obrázek 3 se to jeví jako chybné, ale bližší zkoumání odhalí, že obě osy se otáčejí v opačných směrech, takže existuje kompenzační efekt, který vytváří průměrnou orientaci os, která se nezměnila oproti počátečnímu stavu.
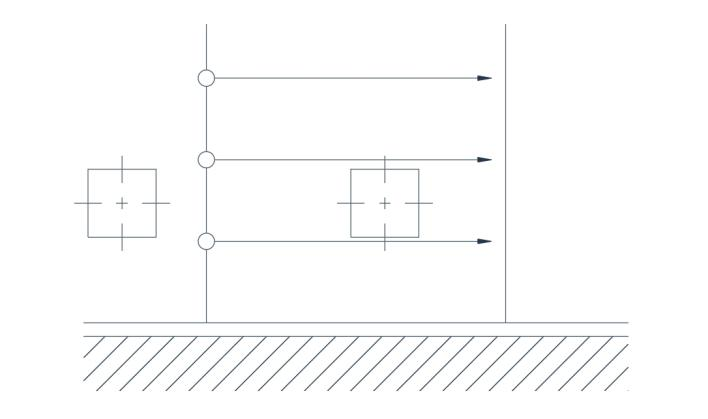
Obr. 2(b) Irotační tok
Protože všechny tekutiny mají viskozitu, proudění skutečné tekutiny nikdy není skutečnou irotací a laminární proudění je samozřejmě vysoce rotační. Irotační proudění je tedy hypotetický stav, který by byl zajímavý pouze z akademického hlediska, nebýt skutečnosti, že v mnoha případech turbulentního proudění jsou rotační charakteristiky tak nevýznamné, že je lze zanedbat. To je výhodné, protože irotační proudění je možné analyzovat pomocí matematických konceptů klasické hydrodynamiky, které byly zmíněny dříve.
Odstředivé čerpadlo mořské vody
Číslo modelu: ASN ASNV
Čerpadla modelů ASN a ASNV jsou jednostupňová odstředivá čerpadla s dvojitým sáním a děleným spirálním tělesem, která se používají k přepravě kapalin ve vodárnách, klimatizačních systémech, budovách, zavlažování, čerpacích stanicích odvodnění, elektrárnách, průmyslových vodovodních systémech, protipožárních systémech, lodích, budovách a tak dále.

Stálý a nestálý tok.
Proudění se nazývá ustálené, když jsou podmínky v jakémkoli bodě konstantní v čase. Přísná interpretace této definice by vedla k závěru, že turbulentní proudění nikdy nebylo skutečně ustálené. Pro daný účel je však vhodné považovat obecný pohyb tekutiny za kritérium a nepravidelné fluktuace spojené s turbulencí pouze za sekundární vliv. Zřejmým příkladem ustáleného proudění je konstantní výtok v potrubí nebo otevřeném kanálu.
Z toho vyplývá, že proudění je nestacionární, když se podmínky mění v čase. Příkladem nestacionárního proudění je proměnlivý výtok v potrubí nebo otevřeném kanálu; obvykle se jedná o přechodný jev, který následuje po ustáleném výtoku nebo je jím následován. Další známé
příklady periodičtější povahy jsou vlnobití a cyklický pohyb velkých vodních ploch v přílivovém proudění.
Většina praktických problémů v hydrotechnice se týká ustáleného proudění. To je štěstí, protože časová proměnná v nestacionárním proudění značně komplikuje analýzu. V této kapitole se proto bude úvaha o nestacionárním proudění omezovat na několik relativně jednoduchých případů. Je však důležité mít na paměti, že několik běžných případů nestacionárního proudění lze na základě principu relativního pohybu redukovat na ustálený stav.
Problém zahrnující plavidlo pohybující se v klidné vodě lze tedy přeformulovat tak, že plavidlo stojí a voda se pohybuje; jediným kritériem pro podobnost chování tekutin je, že relativní rychlost musí být stejná. Vlnný pohyb v hluboké vodě lze opět redukovat na
ustáleného stavu za předpokladu, že se pozorovatel pohybuje s vlnami stejnou rychlostí.

Vertikální drenážní čerpadlo s dieselovým motorem, vícestupňové odstředivé, řadové, s dieselovým motorem, určené pro čerpání odpadních vod bez koroze a s obsahem nerozpuštěných látek (bez vlákniny a drti) nižším než 150 mg/l v odpadních vodách. Vertikální drenážní čerpadlo typu VTP je součástí vertikálních vodních čerpadel typu VTP a na základě zvýšení a límce se maže vodou. Při teplotách pod 60 °C může čerpat odpadní vodu, která obsahuje určité pevné částice (například železný šrot, jemný písek, uhlí atd.).
Rovnoměrný a nerovnoměrný tok.
Proudění se nazývá rovnoměrné, když se velikost a směr vektoru rychlosti nemění z jednoho bodu do druhého podél dráhy proudění. Aby tato definice splňovala požadavky, musí být jak plocha proudění, tak rychlost v každém průřezu stejné. K nerovnoměrnému proudění dochází, když se vektor rychlosti mění s umístěním, typickým příkladem je proudění mezi konvergujícími nebo divergujícími hranicemi.
Obě tyto alternativní podmínky proudění jsou běžné v hydraulice s otevřeným kanálem, ačkoli striktně vzato, protože k rovnoměrnému proudění se vždy přistupuje asymptoticky, jedná se o ideální stav, který je pouze aproximován a nikdy ve skutečnosti není dosažen. Je třeba poznamenat, že podmínky se vztahují spíše k prostoru než k času, a proto jsou v případech uzavřeného proudění (např. potrubí pod tlakem) zcela nezávislé na ustálené nebo nestacionární povaze proudění.
Čas zveřejnění: 29. března 2024
 sales@tkflow.com
sales@tkflow.com 
